From free algebras to free monads
In Universal algebra freeness is a well defined algebraic property. We will explore equational theories which are tightly connected to free algebras. We will consider free monoids. Then we'll explain how monads can be brought into the picture in the context of monoidal categories. This will lead to a precise definition of a free monad as a free monoid.
This post requires familiarity with some very basic Category Theory and does not assume any knowledge on Universal Algebra. Most mathematical notions will be introduced but you might want to dig into literature for some more examples; though most of the books are quite lengthy and not suited for non-mathematicians - you've been warned ;). Knowing this I tried to bring all the required definitions, together with some very basic examples. As you read you may want to read about semigroups, monoids, groups, $G$-sets, lattices, Boolean or Heyting algebras from WikiPedia articles or try to find info on nCatLab (though this is is a heavy resource, with mostly with higher categorical approach, so probably better suited for more familiar readers).
Preliminaries
We will need some preliminary definitions. Let's begin with a definition of algebra. For a set $A$ we will denote $A^n$ the $n$-th cartesian product of $A$, i.e. $A^2=A\times A$.
Definition Algebra
Examples includes many classical algebraic structures, like semigroups, where there is only a single operation of arity 2, monoids which in addition have one operation of arity $0$ - the unit element of multiplication. Other source of examples are Boolean algebras with two 2-ary operations $\wedge$ and $\vee$ or more generally lattices, Heyting algebras. Also rings, modules, fields, vector spaces and countless other structures. Universal algebra has a very general theory describing common concepts but also deals with very special cases of some of more esoteric algebras.
Definition Homomorphism
This means that homomorphism preserve operations. For example a homomorphism of monoids is a map that preserves the multiplication and unit. For boolean algebras, it means that a homomorphism preserves the $\vee$ (also called join) and $\wedge$ (usually called meet) operations, etc.
It is an easy observations that homomorphism are closed under composition and since the identity map is always a homomorphism this leads to well defined categories, e.g. category of monoids, category of boolean algebras, category of rings, ...
Free algebras and Equational theories
Free Algebra
As you can see the definition of a free algebra requires a context, this interesting in its own! There are free monoids in the class of all monoids and there are free commutative monoids in the class of commutative monoids (i.e. monoids in which $m\cdot n=n\cdot m$ for each elements $m,n$).
Many theories allow free algebras. Let's see some other examples:- The monoid of natural numbers $\mathbb{N}$ with addition and $0$ as its unit element is a free monoid generated by $\{1\}$. It is both free in the class of all monoids and in the class of commutative ones. The $n$-th cartesian product $\mathbb{N}^n$ is a free commutative monoid generated by the set $\{(1,0,\ldots,0),(0,1,0,\ldots,0),\ldots,(0,\ldots,0,1)\}$, but it's not a free monoid in the class of all monoids.
- The additive group of integers $\mathbb{Z}$ is a free group with one generator, it is also free in the class of commutative groups. As in monoids: $\mathbb{Z}^n$ is a free commutative group with $n$ generators.
- A free group with two generators can be pictured as the Cayley graph (which is a fractal) (note that its first quarter is the free monoid with two generators).
- Every vector space is free, since every vector space admits a basis.
- In the class of $G$-sets, free $G$ sets are exactly all the cartesian products of $G^n$.
-
In the class of
rings,
polynomial rings with integer coefficients, usually
denoted by: $\mathbb{Z}[X]$ or
$\mathbb{Z}[X_1,\dots,X_n]$ for polynomials with
many variables) are free (you likely have learned
quite a lot about them in
school, you just haven't been told the really
interesting part ;)). This example was the
motivation for terms, their algebra and term
functions which we will discover next.
This is also true for semi-rings. You might have used this fact when using purescript-validation library. A free semiring generated by a type
ahas type[[a]]; for example[[()]]is isomorphic to $\mathbb{N}[X]$, since (please excuse mixing Haskell and mathematical notation): $$[[()]]\simeq[\mathbb{N}]\simeq\mathbb{N}[X]$$
Free algebras play an essential role in a proof of beautiful and outstanding Birkhoff theorem. It states that a class of algebras $\mathcal{C}$ is an equational theory if and only if the class is closed under cartesian products, homomorphic images and subalgebras. Equational theories are classes of algebras which satisfy a set of equations; examples includes: semigroups, monoids, groups or boolean or Heyting algebras but also commutative (abelian) semigroups / monoids / groups, and many other classical algebraic structures.
We need to be a little bit more precise language to speak about equational theories in the full generality of Universal Algebra, which we are going to introduce.
Terms, term functions and their algebra
Definition Term
- each $x\in X$ is a term (of arity $0$)
- each $f_i(x_1,\dots ,x_{j_i})$ is a term of arity $j_i$ for $x_1,\dots ,x_{j_i}\in X$
- if $g_1,\dots g_n$ are terms of arities $j_1$ to $j_n$ respectively, and $g$ is a term of arity $n$ then $g(g_1(x_{11},\dots,x_{1j_1}),\dots, g_n(x_{n1},\dots,x_{nj_n}))$ is a term of arity $j_1+\dots+j_n$ with $x_{kl}\in X$.
We will denote the set of terms on $X$ by $\mathsf{T}^{(f_i)_{i=1,\dots,n}}(X)$ or simply $\mathsf{T}(X)$.
For example in groups: $x^{-1}\cdot x$, $x\cdot y$ and $1$ (the unit of the group) are terms. Terms are just abstract expressions that one can build using algebraic operations that are supported by the algebra type. Each term $t$ defines a term function on every algebra of the given type. In groups the following terms are distinct but they define equal term function: $x^{-1}\cdot x$ and $1$; on the other hand the two (distinct) terms $(x\cdot y)\cdot z$ and $x\cdot (y\cdot z)$ define equal term functions. The two terms $x\cdot y$ and $y\cdot x$ define distinct term functions (on non commutative groups or commutative monoids). Another example comes from boolean algebras (or more broadly lattice theory) where the two terms $x\wedge (y\vee z)$ and $(x\wedge y)\vee(x\wedge z)$ define equal term functions on Boolean algebras (or more generally distributive lattices). If $t$ is a term then the associated term function on an algebra $\underline{A}$ we let denote by $\tilde{t}^{\underline{A}}$. Term functions are natural to express equalities within a theory. Now we are ready to formally define equational classes of algebras.
Definition Equational Theory
For example the class of monoids is an equational theory for $$\mathbf{E}=\bigl\{(1\cdot x,\, x),\; (x\cdot 1,\, x),\; \bigl((x\cdot y)\cdot z,\, x\cdot (y\cdot z)\bigr)\bigr\}$$ i.e. all the algebras with two operations: one of arity 0 (the unit) and one of arity 2 (the multiplication), such that the $1$ is the unit for multiplication $\cdot $ and multiplication is associative. The class of commutative monoids is also an equational theory with one additional equation $(x\cdot y,\, y\cdot x)$. Groups, Boolean or Heyting algebras, lattices are also equational theories.
Coming back to free algebras: it turns out that the set of terms $\mathsf{T}^{(f_i)}(X)$ on a given set of variables $X$ has an algebra structure of type $(f_i)_{i=1,\dots,n}$: it is given by the inductive step in the definition of terms: if $t_i\in \mathsf{T}^{(f_i)}(X)$ for $i=1,\dots,j_i$ then $$ f_j^{\underline{\mathsf{T}^{(f_i)}(X)}}(t_1,\ldots,t_{j_i}) := f_j(t_1,\ldots,t_{j_i})\in \mathsf{T}(X) $$ Furthermore $\underline{\mathsf{T}^{(f_i)}(X)}$ is a free algebra over $X$ in the class of all algebras of the given type $(f_i)_{i=1,\dots,n}$. An extension of a map $h:X\rightarrow\underline{A}=(A,(f_i^{\underline{A}})_{i=1,\ldots,n})$ can be build inductively following the definition of terms and using the homomorphism property: $$ h(f_i(t_1,\ldots,f_{i_j})) := f_i^{\underline{A}}(h(t_1),\ldots,h(t_{i_j})) $$ The map $h$ is indeed a homomorphism: $$ \begin{array}{ll} h\bigl(f_i^{\underline{\mathsf{T}(X)}}(t_1,\ldots,t_{i_j})\bigr) & = h(f_i(t_1,\ldots, t_{i_j}) \\\\ & = f_i^{\underline{A}}(h(t_1),\ldots, h(t_{i_j})) \\\\ \end{array} $$ Note that the class of algebras of the same type is usually very broad, but this is the first approximation to build free algebras in an equational theory. This is just the equational theory for the empty set $\mathbf{E}$.
Let’s see this on an example and let us consider algebras
of the same type as a monoid: with one nullary operation
(unit $1$ or mempty if you like) and one 2-ary
operation (multiplication / mappend). Let $X$
be a set of variables. Then $1$ is a valid term, and also
if $t_1$ and $t_2$ are terms on $X$ then also $t_1\cdot
t_2$ is a term, but also $t_1\cdot 1$ and $1\cdot t_2$ are
valid and distinct terms. $\mathsf{T}(X)$ resembles
a monoid but it isn't. It is not associative and the
unitality condition is not valid since $t\cdot 1\neq
t\neq 1\cdot t$ as terms. We still need a way to enforce
the laws. But note that if you have a map
$f:X\rightarrow M$ to a monoid $M$ which you'd like to extend to
a homomorphism $\mathsf{T}(X)\rightarrow M$ that preserves
$1$ (which is not the unit, yet) and multiplication (even
though it is not associative), you don’t have much choice:
$\mathsf{T}(X)\rightarrow M$: $t_1\cdot t_2$ must be mapped
to $f(t_1)\cdot f(t_2)\in M$.
We need a tool to enforce term equations. For that one can use
Definition Congruence relation
- reflexive: for each $a\in A$: $a\sim a$
- symmetric: for each $a,b\in A$: if $a\sim b$ then $b\sim a$
- transitive: for each $a,b,c\in A$: if $a\sim b$ and $b\sim c$ then $a\sim c$
Equivalence relations and congruences form complete lattices (partial ordered which have all suprema and minima, also infinite). If you have two equivalence relations (congruences) then their intersection (as subsets of $A^2$) is an equivalence relation (congruence).
The set of equations that defines the class of monoids generates a congruence relation on the term algebra $\underline{\mathsf{T}^{f_i}(X)}$ (i.e. an equivalence relation which is compatible with operations: $x_1\sim y_1$ and $x_2\sim y_2$ then $(x_1\cdot y_1) \sim (x_2\cdot y_2)$). One can define it as the smallest congruence relation which contains the set $\mathbf{E}$. Equivalence relation on a set $A$ is just a subset of the cartesian product $A\times A$ (which satisfy certain axioms), so it all fits together! One can describe this congruence more precisely, but we'll be happy with the fact that it exists. To show that, first one need to observe that intersection of congruences is a congruence, then the smallest congruence containing the set $\mathbf{E}$ is an intersection of all congruences that contain $\mathbf{E}$. This intersection is non empty since the set $A\times A$ is itself a congruence relation.
The key point now is that if we take the term algebra and take a quotient by the smallest congruence that contains all the pairs of terms which belong to the set $\mathbf{E}$ we will obtain a free algebra in the equational class defined by $\mathbf{E}$. We will leave the proof to a curious reader.
Free monoids
Let’s take a look on a free monoid that we can build this way. First let us consider the free algebra $\underline{\mathsf{T}(X)}$ for algebras of the same type as monoids (which include non associative monoids, which unit does not behave like a unit). And let $\sim$ be the smallest relation (congruence) that enforces $\mathsf{T}(X)/\sim$ to be a monoid.
Since monoids are associative every element in $\underline{\mathsf{T}(X)}/\sim$ can be represented as $x_1\cdot( x_2\cdot (x_3\cdot\ldots \cdot x_n))$ (where we group brackets to the right). Multiplication of $x_1\cdot( x_2\cdot (x_3\cdot\ldots \cdot x_n))$ and $y_1\cdot( y_2\cdot (y_3\cdot\ldots \cdot y_m))$ is just $x_1\cdot (x_2\cdot (x_3\cdot\ldots\cdot(x_n\cdot (y_1\cdot (y_2\cdot (y_3\cdot\ldots\;\cdot y_m)\ldots)$. In Haskell if you’d represent the set $X$ as a type $a$ then the free monoid is just the list type $[a]$ with multiplication: list concatenation and unit element: the empty list. Just think of
-- A set with `n` elements corresponds -- to a type with `n` constructors: data X = X_1|⋯|X_n
Free Monads
It turns out that monads in $\mathcal{Hask}$ are also an equational theory. Just the terms are higher kinded: $*\rightarrow*$ rather than $*$ as in monoids. The same construction of a free algebra works in the land of monads, but we need to look at them from another perspective. Let us first take a mathematical definition of view on monads.
Definition Monad
m
with two
natural transformations:
class Monad m where return :: a -> m a join :: m(m a) -> m awhich is unital and associative, i.e. the following law holds:
-- | associativity join . join == join . fmap join -- | unitality join . return = id = join . fmap return
These axioms are easier to understand as diagrams:
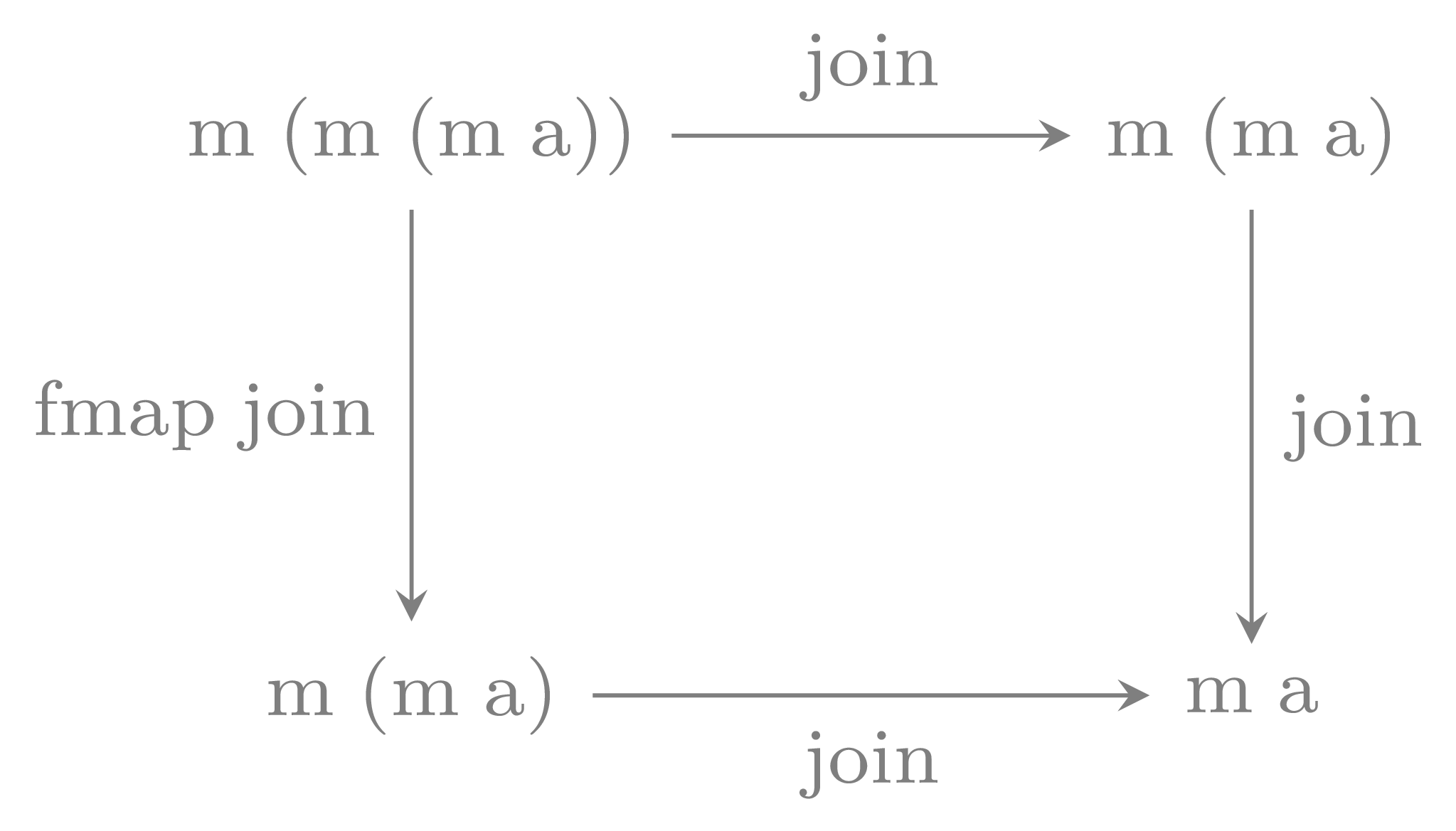
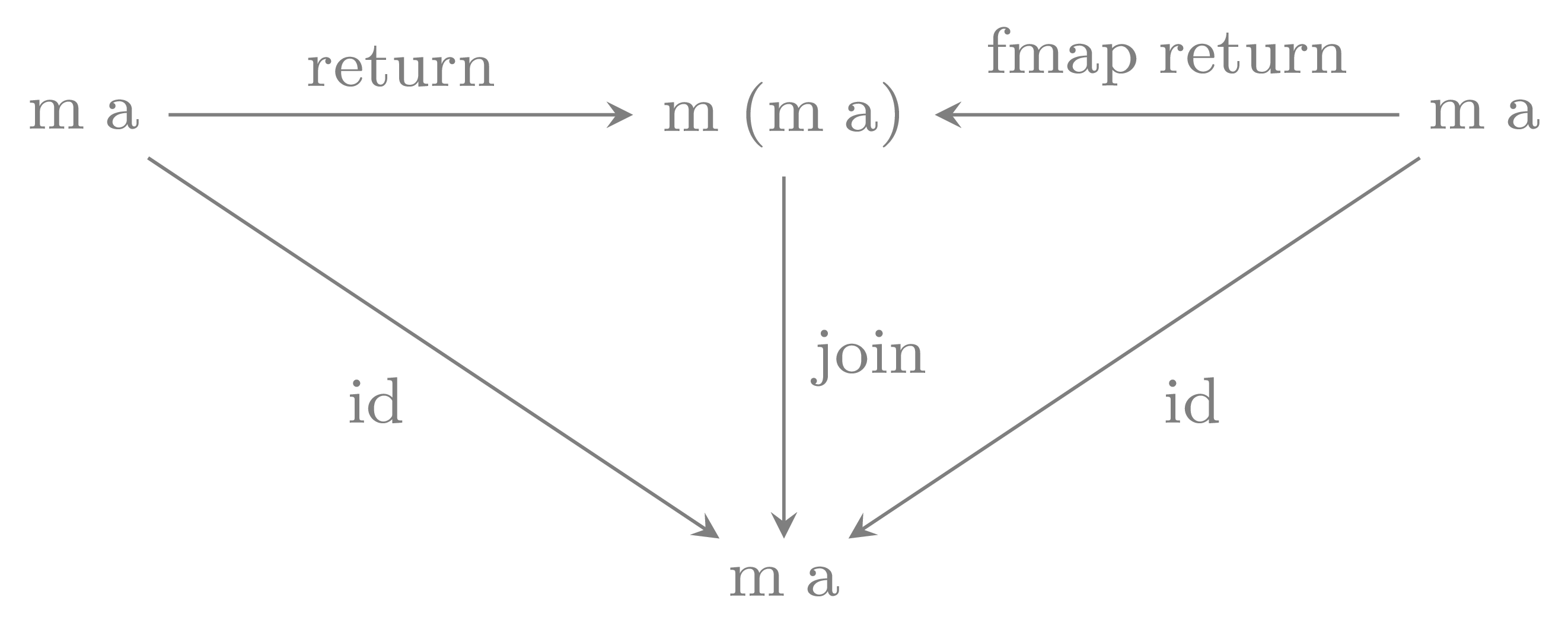
It is a basic lemma that this definition a monad is equivalent to what we are used to in Haskell:
class Monad m where return :: a -> m a >>= :: m a -> (a -> m b) -> m b
Having join one defines >>= as
ma >>= f = join $ f <$> maand the other way, having >>= then
join = (>>= id)`Not only these two constructions are reverse to each other, but also they translate the monad laws correctly.
Monoids in monoidal categories
To define a monoid $M$ in the category $\mathcal{Set}$ (of sets) one needs the product $M\times M$. Abstraction of this structure leads to monoidal categories.Definition Monoidal Category
Most examples of monoidal categories are not strict but are associative and unital up to a natural transformation. Think of $(A\times B)\times C\simeq A\times(B\times C)$ in $\mathcal{Set}$ (or any category with (finite) products, like $\mathcal{Hask}$). Let me just stress out that since $\otimes$ is a bifunctor, for any two maps $f:\;a_1\rightarrow b_1$ and $g:\;a_2\rightarrow b_2$ we have a map $f\otimes g: a_1\otimes a_2\rightarrow b_1\otimes b_2$, and moreover it behaves nicely with respect to composition: $(f_1\otimes g_1) \cdot (f_2\otimes g_2) = (f_1\cdot f_2)\otimes(g_1\cdot g_2)$ for composable pairs of arrows $f_1,\;f_2$ and $g_1,\;g_2$.
Now we can generalise a definition of a monoid to such categories:
Definition Monoid in a Monoidal Category
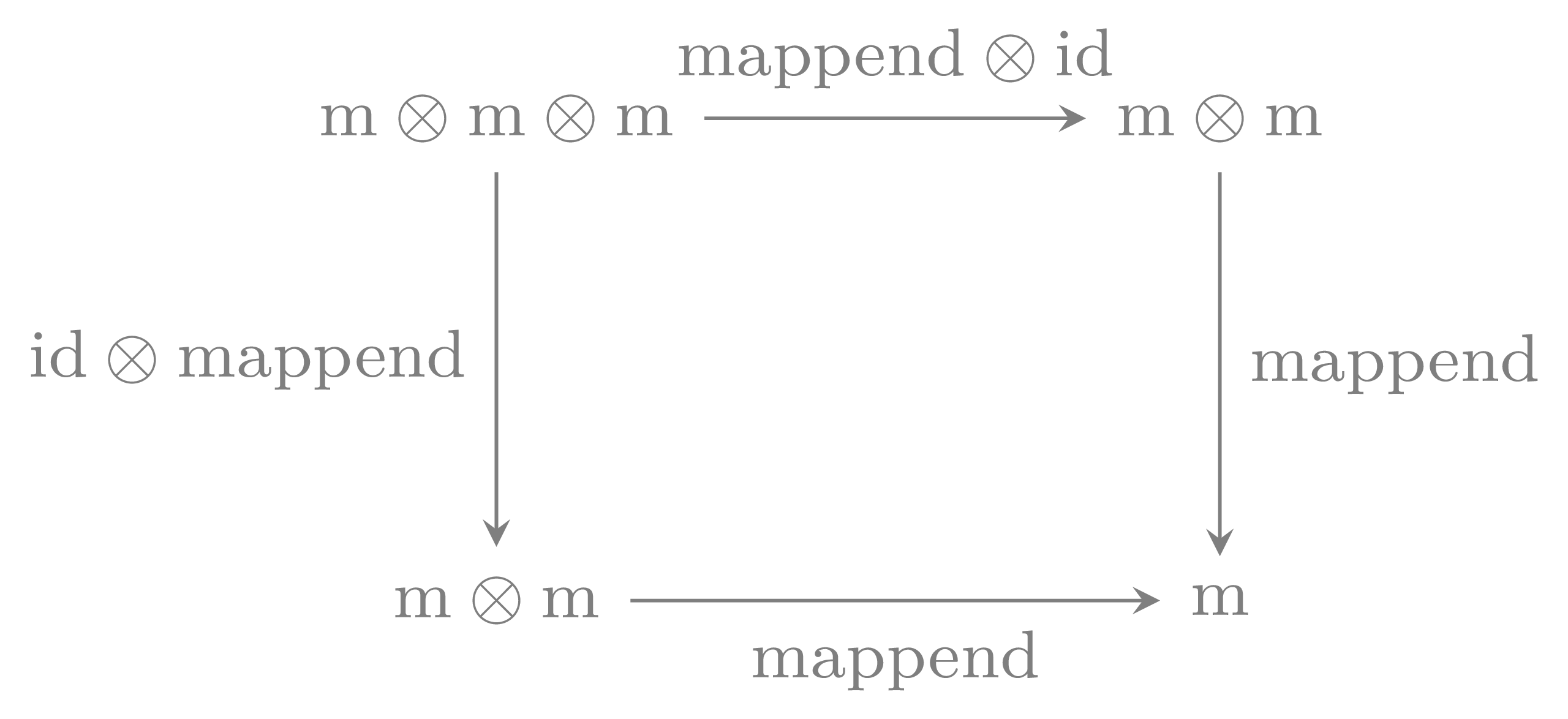
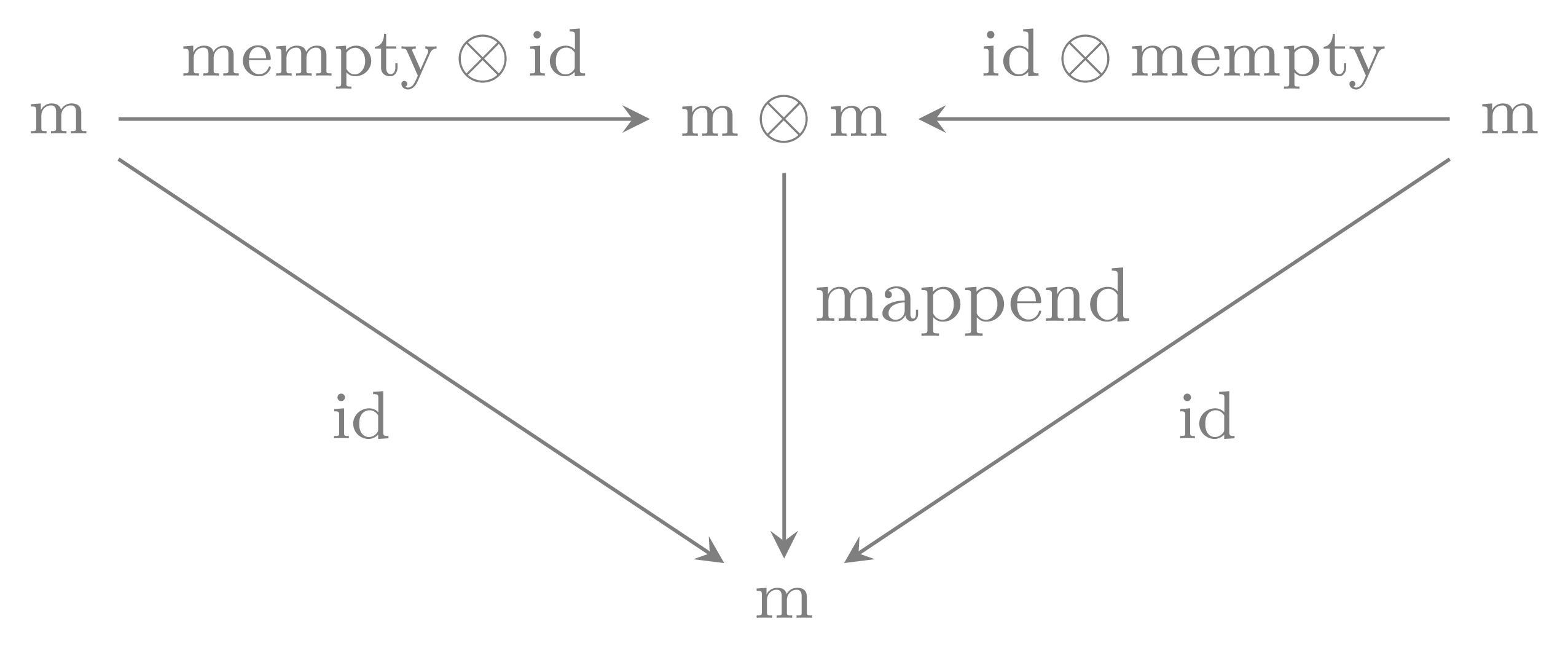
The main point of this section is that these diagrams have exactly the same shape as associativity and unitality for monads. Indeed, a monoid in the category of endo-functors with functor composition as a monoidal product $\otimes$ and unit the identity functor is a monad. In category theory this category is strict monoidal, if you try to type this in Haskell you will end up with a non strict monoidal structure, where you will need to show penthagon equation.
These consideration suggest that we should be able to build a free monad using our algebraic approach to free algebras. And this is what we will follow in the next section.
Free monads in $\mathcal{Hask}$
Firstly, what should replace the set of generators $X$ in
$\mathsf{T}(X)/\sim$?
First we generalised from the category of sets $\mathcal{Set}$ to
a monoidal category $(\mathcal{C},\otimes, 1)$: its clear
that we just should pick an object of the category
$\mathcal{C}$. Now since our category is the category of
(endo) functors of $\mathcal{Hask}$ the set of generators
is just a functor. So let's pick a functor f.
To get a free monad we need to decypher $\mathsf{T}(f)/\sim$ in the context of a monoid in a monoidal category of endofunctors. Note that here $\mathsf{T}(f)$ and $\mathsf{T}(f)/\sim$ are functors! To simplify the notation, let $\mathsf{Free}(f):=\mathsf{T}(f)/\sim$. So what is a term in this setting? It should be an expressions of a Haskell's type: $$ \begin{equation} \begin{array}{c} \bigl(\mathsf{Free}(f)\otimes\mathsf{Free}(f)\otimes\ldots\otimes \mathsf{Free}(f)\bigr)(a) \\\\ \quad\quad = \mathsf{Free}(f)\bigl(\mathsf{Free}(f)\bigl(\ldots (\mathsf{Free}(f)(a)\bigr)\ldots\bigr) \end{array} \end{equation} $$ In our setup the monoidal product $-\otimes-$ is just the functor composition, thus $\mathsf{Free}(f)(a)$ must be a type which (Haskell's) terms are of Haskell's types:
a, f a, f (f a), f (f (f a)), ...
The monadic join will take something of
type $\mathsf{Free}(f)\;(\mathsf{Free}(f)\;(a))$, e.g. $f^n(b)=f\;(f\;(\dots f\;(b)\dots)$ (by abusing the notation $f^n$)
where $b$ has type
$f^m(a)=(f\;(f\;(\dots(f\;(a)\dots)$ and return something
of type $\mathsf{Free}(f)(a)$ and it should be quite clear
how to do that: just take the obvious element of type
$f^{n+m}(a)$. Altogether, this is a good trace of a monad,
so let us translate this into a concrete Haskell type:
data Free f a = Return a -- ^ the terms of type a | Free (f (Free f a)) -- ^ -- recursive definition which embraces -- `f a`, `f (f a)` and so on instance Functor f => Functor (Free f) where fmap f (Return a) = Return (f a) fmap f (Free ff) = Free (fmap (fmap f) ff)
Free f is just a tree shaped by the functor
f. This type indeed embraces all the terms of
types: a, f a, f (f a), ... into a single
type. Now the monad instance:
instance Monad (Free f a) where return = Return join (Return ma) = ma -- ^ stitch a tree of trees into a tree join (Free fma) = Free $ join <$> fma -- ^ recurs to the leaves
As you can see, takes a tree of trees and outputs a bigger
tree, that's what join does on the
Return constructor.
Before formulating the next result let's describe morphisms
between monads. Let m and n be
two monads then a natural transformation
f :: forall a. m a -> n a is a homomorphism of monads iff the
following two conditions are satisfied:
f . return == return
join . f == f . fmap f . join
Note that this two conditions are satisfied iff
f is a monoid homomorphism in the category of (endo)functors
of $\mathcal{Hask}$.
Proposition
Letf be a functor, then Free
f then there exists a morphism:
foldFree :: Functor f => (forall x. f x -> m x) -> (Free f a -> m a)which restricts to an isomorphism of natural transformations on the left hand side and monad homomorphisms on the right hand side, and thus
Free f is rightly colled free monad..
Proof
Let start with a definition offoldFree.
foldFree :: Functor f => (forall x. f x -> m x) -> (Free f a -> m a)
foldFree _ (Return a) = return a
foldFree f (Free ff) = join $ f $ foldFree f <$> ffliftF :: Functor f => (forall x. Free f x -> m x) -> (f a -> m a) liftF f fa = f $ Free $ Return <$> faFirst let's check that
foldFree f is a morphism of monads:
foldFree f (Return a) -- | by definition of (foldFree f) = return a foldFree f (join (Return a)) = foldFree f a -- | by monad unitality axiom = join $ return $ foldFree f $ a -- | by definition of (foldFree f) = join $ foldFree f (Return $ foldFree f a) -- | by definition of functor instance of (Free f) = join $ foldFree f $ fmap (foldFree f) $ Return a foldFree f (join (Free ff) -- | by definition of join for (Free f) = foldFree f (Free $ fmap join $ ff) -- | by definition of foldFree = join $ f $ fmap (foldFree f) $ fmap join $ ff = join $ f $ fmap (foldFree f . join) $ ff -- | by induction hypothesis = join $ f $ fmap (join . foldFree f . fmap (foldFree f)) $ ff = join $ f $ fmap join $ fmap (foldFree f) $ fmap (fmap (foldFree f)) $ ff -- | f is natural transformation = join $ fmap join $ f $ fmap (foldFree f) $ fmap (fmap (foldFree f)) $ ff -- | monad associativity = join $ join $ f $ fmap (foldFree f) $ fmap (fmap (foldFree f)) $ ff -- | by definition of (foldFree f) = join $ foldFree f $ Free $ fmap (fmap (foldFree f)) $ ff -- | by functor instance of (Free f) = join $ foldFree f $ fmap (foldFree f) $ Free ffAnd we have
foldFree . liftF :: (forall x. Free f x -> m x) -> (Free f a -> m a) (foldFree . liftF $ f) (Return x) -- ^ where f is a morphism of monads = foldFree (liftF f) (Return x) = return x = f (Return x) -- since f is assumed to be a morphism of monads (foldFree . liftF $ f) (Free ff) -- ^ where f is a morphism of monads = foldFree (liftF f) (Free ff) = join $ liftF f $ fmap (foldFree (liftF f)) $ ff -- | by induction hypothesis = join $ liftF f $ fmap f $ ff -- | by definition of (liftF f) = join $ f $ Free $ fmap Return $ fmap f $ ff -- | by functor instance of (Free f) = join $ f $ fmap f $ Free (Return ff) -- | since f is a morphism of monads = f $ join $ Free (Return ff) = f $ Free ff
liftF . foldFree :: (forall x. f x -> m x) -> (f a -> m a) (liftF . foldFree $ f) fa -- ^ where f is a natural transformation = liftF (foldFree f) $ fa -- | by definition of liftF = (foldFree f) $ Free $ fmap Return $ fa -- | by definition of (foldFree f) = join $ f $ fmap (foldFree f) $ fmap Return $ fa = join $ f $ fmap (foldFree f . Return) $ fa -- | by definition of (foldFree f) = join $ f $ fmap return $ fa -- | since f is a natural transformation = join $ fmap return $ f fa -- | by monad unitality axiom = f fa
foldFree corresponds to foldMap which is
defined in a very similar way
foldMap :: Monoid m => (a -> m) -> [a] -> m
foldMap _ [] = mempty
foldMap f (a : as) = mappend (f a) (foldMap f as)foldMap is an isomorphism onto
monoid homomorphisms with an inverse
g :: Monoid m => ([a] -> m) -> a -> m g f a = f [a]
Furthermore, if we had polymorphic functions over monoidal
categories in our type system, foldMap and
foldFree would be specialisations of the
same function!
Some examples of free monads
Let us study some simple examples of free monads-
First let us consider the constant functor:
data Const a b = Const a
ThenFree (Const a)is isomorphic toEither atoEither :: Free (Const a) b -> Either a b toEither (Return b) = Right b toEither (Free (Const a)) = Left a fromEither :: Either a b -> Free (Const a) b fromEither (Right b) = Return b fromEither (Left a) = Free (Const a)SinceEither ()is isomorphic withMaybealsoMaybeis a free monad. -
Free Identityis isomorphic to:
Note thatdata Nat = Zero | Succ Nat newtype Writer m a = Writer { runWriter :: (m, a) } deriving Functor toFree1 :: Free Identity a -> Writer Nat a toFree1 (Return a) = Writer (Zero, a) toFree1 (Free (Identity fa)) = case toFree1 fa of Writer (n, a) -> (Succ n, a) fromFree1 :: (Nat, a) -> Free Identity a fromFree1 (Writer (Zero, a)) = Return a fromFree1 (Writer (Succ n, a)) = Free (Identity (fromFree1 (Free1 n a)))Natis the free monoid with one generator (Nat$\simeq$[()]) in the cateogry $\mathcal{Hask}$, and so isFree Identitybut in the monoidal category of endofunctors of $\mathcal{Hask}$! -
If you take a functor with two constructors
data F2 a = FX a | FY a deriving Functor
. Then we havedata S2 = SX | SY toFree2 :: Free F2 a -> Writer [S2] a toFree2 (Return a) = Writer ([], a) toFree2 (Free (FX fa)) = case toM2 fa of Writer (m, a) -> Writer (SX : m, a) toM2 (Free (FY fa)) = case toM2 fa of Writer (m, a) -> Writer (SY : m, a) fromFree2 :: Writer [S2] a -> Free F2 a fromFree2 (Writer ([], a)) = Return a fromFree2 (Writer (SX : xs, a)) = Free (FX (fromM2 $ Writer (xs, a))) fromFree2 (Writer (SY : xs, a)) = Free (FY (fromM2 $ Writer (xs, a)))
toFree2andfromFree2are isomorphisms. I think you see the pattern: if you take a functor with $n$ constructors you will end up with a writer monad over a free monoid with $n$ generators. You might ask if all the monads are free then? The answer is no: take a non free monoidmthen the monadWriter mis a non free monad. You can prove your self that the writer monadWriter mis free if and only if the monoidmis a free monoid in $\mathcal{Hask}$.
Final remarks
I hope I convinced you that monads are algebraic constructs and I hope you'll find universal algebra approach useful. In many cases we are dealing with algebraic structures which we require to satisfy certain equations. Very often they fit into equational theories, which have a very clear description and which allow free objects. Freeness is the property that lets one easily interpret the free object in any other object of the same type. In the monad setting they are really useful when writing DSLs, since you will be able to interpret it in any monad, like IO or some pure monad.
References
- A Course in Universal Algebra by S. Burris, H.P. Sankappanavar
- Universal Algebra by G. Grätzer
- Category Theory for Computing Science by M.Barr and C.Wells